Laplace PDE: Neumann Problem on a Rectangle

Laplace PDE:

\[\Delta u = 0 \qquad \left( \Delta u = u_{xx} + u_{yy} \right)\]

Product Solution:

Assume $u(x, y) = X(x) Y(y)$.

$c=0$:

\[u = (d_1 y + d_2) (c_1 x + c_2)\]

$c=\lambda^2, \lambda > 0$

\[u = \left[ d_1 \sin(\lambda y) + d_2 \cos(\lambda y) \right] \left[ (c_1 \sinh(\lambda x) + c_2 \cosh(\lambda x) \right]\]

$c=-\lambda^2, \lambda > 0$

\[u = \left[ d_1 \sinh(\lambda y) + d_2 \cosh(\lambda y) \right] \left[ (c_1 \sin(\lambda x) + c_2 \cos(\lambda x) \right]\]

Neumann Boundary Problem on a Rectangle:

Non-Zero Bottom Edge:

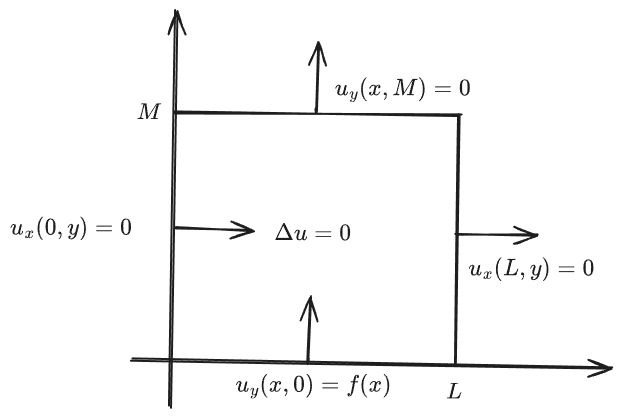
Problem:

\[\Delta u = 0 \qquad x \in (0, L), \ y \in (0, M)\] \[u_y(x, 0) = f(x) \qquad u_y(x, M) = 0\] \[u_x(0, y) = 0 \qquad u_x(L, y) = 0\]

Considering the BC:

\[u_x(0, y) = u_x(L, y) = 0 \implies X'(0) = X'(L) = 0\]

$c = 0$:

\[X = c_1 x + c_2\] \[X' = c_1 = 0\] \[X = 1\] \[u = d_1 y + d_2\]

$c = \lambda^2$:

\[X = c_1 \sinh(\lambda x) + c_2 \cosh(\lambda x)\] \[X' = c_1 \lambda \cosh(\lambda x) + c_2 \lambda \sinh(\lambda x)\] \[X'(0) = c_1 \lambda = 0 \implies c_1 = 0\] \[X'(L) = c_2 \lambda \sinh(\lambda L) = 0 \implies c_2 = 0\] \[X = 0, \ u = 0, \ \text{trivial solution}\]

$c = -\lambda^2$:

\[X = c_1 \sin(\lambda x) + c_2 \cos(\lambda x)\] \[X' = c_1 \lambda \cos(\lambda x) - c_2 \lambda \sin(\lambda x)\] \[X'(0) = c_1 \lambda = 0 \implies c_1 = 0\] \[X'(L) = - c_2 \lambda \sin(\lambda L) = 0 \implies \lambda_n = \frac{n \pi}{L}\] \[X_n = \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\] \[u_n = \left[ d_1 \sinh(\lambda_n y) + d_2 \cosh(\lambda_n y) \right] \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\]

Considering the BC:

\[u_y(x, M) = 0 \implies Y'(M) = 0\]

$c = 0:$

\[Y = d_1 y + d_2\] \[Y' = d_1 = 0 \implies Y = 1 \qquad u_0 = 1\]

$c = - \lambda^2:$

\[Y = d_1 \sinh(\lambda_n y) + d_2 \cosh(\lambda_n y)\] \[Y' = d_1 \lambda_n \cosh(\lambda_n y) + d_2 \lambda \sinh(\lambda_n y)\] \[Y'(M) = d_1 \lambda_n \cosh(\lambda_n M) + d_2 \lambda \sinh(\lambda_n M) = 0\] \[d_1 = -\sinh(\lambda_n M) \qquad d_2 = \cosh(\lambda_n M) = 0\] \[Y = -\sinh(\lambda_n M) \sinh(\lambda_n y) + \cosh(\lambda_n M) \cosh(\lambda_n y)\] \[Y = \cosh \left[ \lambda_n (M - y) \right]\] \[u_n = \cosh \left[ \lambda_n (M - y) \right] \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\]

So:

\[u = a_0 + \sum_{n=1}^\infty a_n \cosh \left[ \lambda_n (M - y) \right] \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\]

Non-Zero Top Edge:

\[u_y(x, 0) = 0 \qquad u_y(x, L) = g(x)\]

Same BC for $u_x(0, y) = u_x(L, y) = 0$, so we still have :

\[u_0 = d_1 y + d_2\] \[u_n = \left[ d_1 \sinh(\lambda_n y) + d_2 \cosh(\lambda_n y) \right] \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\]

Considering the BC:

\[u_y(x, 0) = 0 \implies Y'(0) = 0\]

$c = 0:$

\[Y = d_1 y + d_2\] \[Y' = d_1 = 0 \implies Y = 1\] \[u_0 = 1\]

$c = \lambda^2:$

\[Y = d_1 \sinh(\lambda_n y) + d_2 \cosh(\lambda_n y)\] \[Y' = d_1 \lambda_n \cosh(\lambda_n y) + d_2 \lambda_n \sinh(\lambda_n y)\] \[Y'(0) = d_1 \lambda_n = 0 \implies d_1 = 0\] \[Y = \cosh(\lambda_n y)\] \[u_n = \cosh(\lambda_n y) \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\]

Non-Zero Left and Right Edges:

Just swap x and y.

$u_x(0, y) = h(y) \qquad u(L, y) = 0$:

\[u_n = \cosh(\gamma_n (L - x)) \cos(\gamma_n y) \qquad \gamma_n = \frac{n \pi}{M}\]

$u(0, y) = 0 \qquad u(L, y) = k(y)$:

\[u_n = \cosh(\gamma_n x) \cos(\gamma_n y) \qquad \gamma_n = \frac{n \pi}{M}\]

Generalizing:

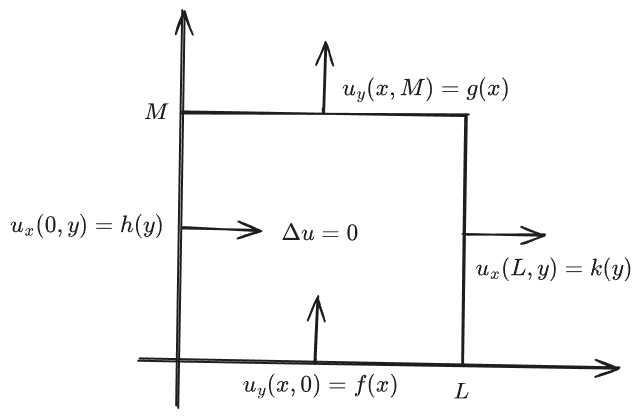
Problem:

\[\Delta u = 0 \qquad x \in (0, L), \ y \in (0, M)\] \[u_y(x, 0) = f(x) \qquad u_y(x, M) = g(x)\] \[u_x(0, y) = h(y) \qquad u_x(L, y) = k(y)\]

By Linearity:

\[u = u^1 + u^2 + u^3 + u^4\]

Where

\[u^1_y(x, 0) = f(x) \qquad u^2_y(x, M) = g(x)\] \[u^3_x(0, y) = h(y) \qquad u^4_x(L, y) = k(y)\]

And

\[u_0 = 1\] \[u_n^1 = \cosh \left[ \lambda_n (M - y) \right] \cos(\lambda_n x) \qquad \lambda_n = \frac{n \pi}{L}\] \[u_n^2 = \cosh(\lambda_n y) \cos(\lambda_n x)\] \[u_n^3 = \cosh(\gamma_n (L - x)) \cos(\gamma_n y) \qquad \gamma_n = \frac{n \pi}{M}\] \[u_n^4 = \cosh(\gamma_n x) \cos(\gamma_n y)\]

Uniqueness

$u_1, u_2 \text{ are sols of Neumann Problem, then } u_1 - u_2 = \text{ const}$.

i.e. solutions to the Neumann Problem differ only by a constant.